知识图谱学习记录

1 知识图谱简述

知识图谱，即一种特殊的语义网络，它利用实体、关系、属性这些基本单位，以符号的形式描述了物理世界中不同的概念和概念之间的相互关系。知识图谱的相关技术已经在搜索引擎、智能问答、语言理解、推荐计算、大数据决策分析等众多领域得到广泛的实际应用。近年来，随着自然语言处理、深度学习、图数据处理等众多领域的飞速发展，知识图谱在自动化知识获取、知识表示学习与推理、大规模图挖掘与分析等领域又取得了很多新进展。知识图谱已经成为实现认知层面的人工智能不可或缺的重要技术之一。

2 知识存储形式

知识图谱数据存储的核心思想是如何存储实体与实体之间产生的联系，对于关系型数据库，常见的有三元组（SPO）、水平表、属性表等，但关系型数据库在大规模遍历关系数据（较深关系）时不能提供高效的性能，故采用原生图数据库 Neo4j 来存储知识图谱的实体、实体间的关系以及属性。基于图数据库构建的知识图谱在博客《Neo4j+陶瓷多模态知识图谱构建》中会进行较为详细的介绍。

3 知识图谱嵌入（Knowledge Graph Embedding）

3.1 概念与优点

在词向量的启发下，研究者考虑如何将知识图谱中的实体和关系映射到连续的向量空间，并包含一些语义层面的信息，可以使得在下游任务中更加方便地操作知识图谱，例如问答任务、关系抽取等。对于计算机来说，连续向量的表达可以蕴涵更多的语义，更容易被计算机理解和操作。将知识图谱中包括实体和关系的内容映射到连续向量空间方法的研究领域称为知识图谱嵌入。

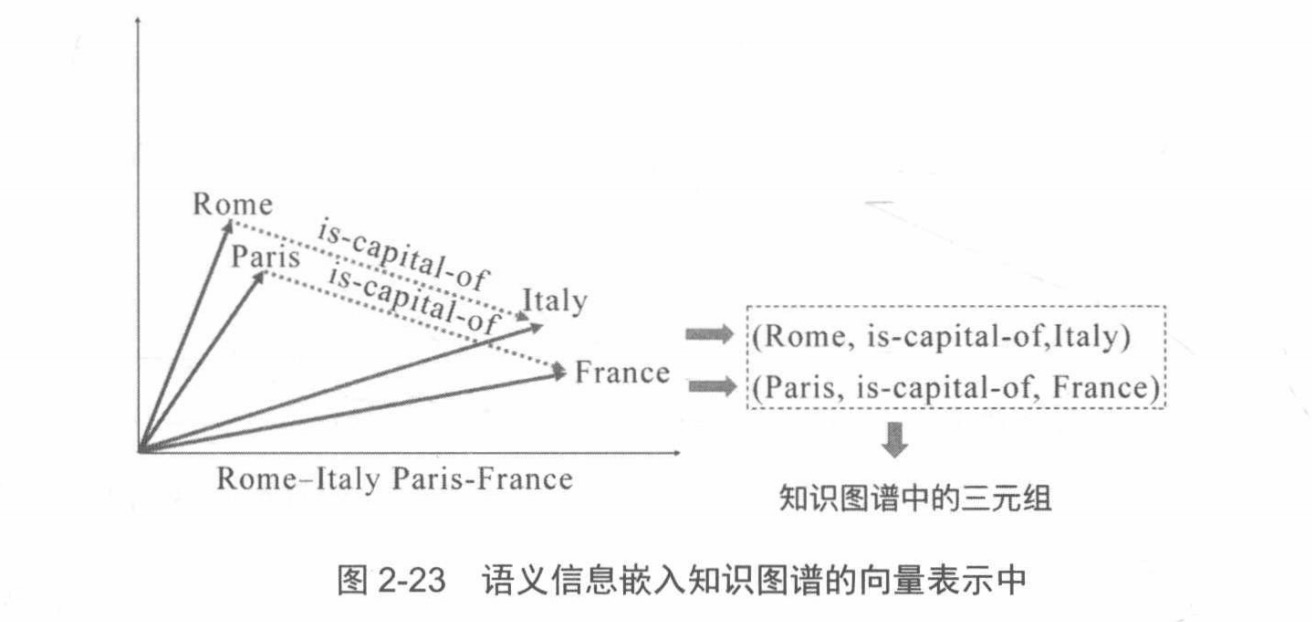
使用向量的表达方式可以提高应用时的计算效率，当把知识图谱的内容映射到向量空间时，相应的算法可以使用数值计算，所以计算的效率也会同时提高。

增加了下游应用设计的多样性。用向量表示后，知识图谱将更加适用于当前流行的机器学习算法，例如神经网络等方法。因为下游应用输入的并不再是符号，所以可以考虑的方法也不会仅局限于图算法。

3.2 知识图谱的嵌入方法

3.2.1 距离转移模型（以 TranE 为例）

论文地址：https://proceedings.neurips.cc/paper/2013/file/1cecc7a77928ca8133fa24680a88d2f9-Paper.pdf

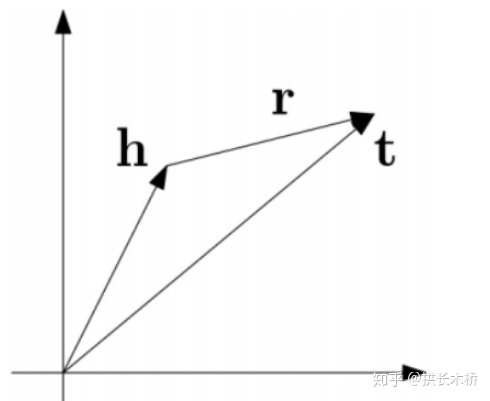
转移距离模型（Translational Distance Model）的主要思想是将衡量向量化后的知识图谱中三元组的合理性问题，转化成衡量头实体和尾实体的距离问题。TransE 模型的基本思想就是把 relation 看做是 head 到 tail 的翻译，认为一个正确的知识三元组应该满足，而错误的不满足。

定义距离公式如下：

定义损失函数如下：

上式表示被破坏的三元组，其中 head 实体或者 tail 实体被随机实体替换作为对照组。训练模型时，期望原三元组损失函数更小，被破坏的三元组损失函数更大。

3.3 一些常用的知识图谱数据集

WN18：https://paperswithcode.com/dataset/wn18
FB15K：https://paperswithcode.com/dataset/fb15k

4 知识图谱的推理

4.1 推理的概念

面向知识图谱的推理主要围绕关系的推理展开，即基于图谱中已有的事实或关系推断出未知的事实或关系，一般着重考察实体、关系和图谱结构三个方面的特征信息。

推理任务主要有：通过规则挖掘对知识图谱进行补全（Knowledge Base Completion,KBC）与质量校验、链接预测、关联关系推理与冲突检测等。

4.2 推理的方法

4.2.1 基于分布式表示推理

常见的方法有：TransE（Translating Embedding）系列算法、RESCAL、DistMul等，可用于下游任务如节点分类、链接预测等。不是个人项目的重点，此处不再展开。

4.2.2 基于神经网络的推理（R-GCN）

Modeling Relational Data with Graph Convolutional Networks：（https://arxiv.org/abs/1703.06103）。本论文将GCN框架应用于关系数据建模，特别是链路预测和实体分类任务。

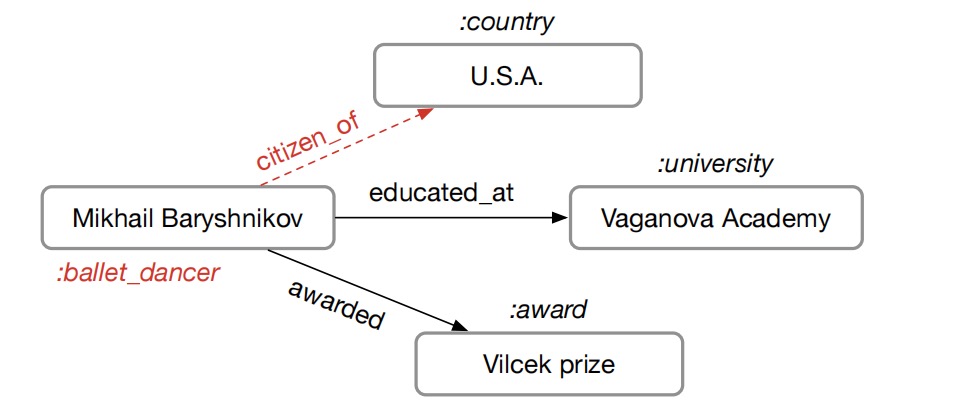
这是论文中给出的一个较为直观的样例，上图中红色字体所在的边和顶点就是链路预测和定点分类，已有关系是Mikhail在Vaganova大学接受教育，通过学校所在地可以推测Mikhail与USA的关系是citizen of。同样通过Mikhail获得过Vilcek奖以及该奖所在领域来推测Mikhail的节点分类是ballet_dancer。

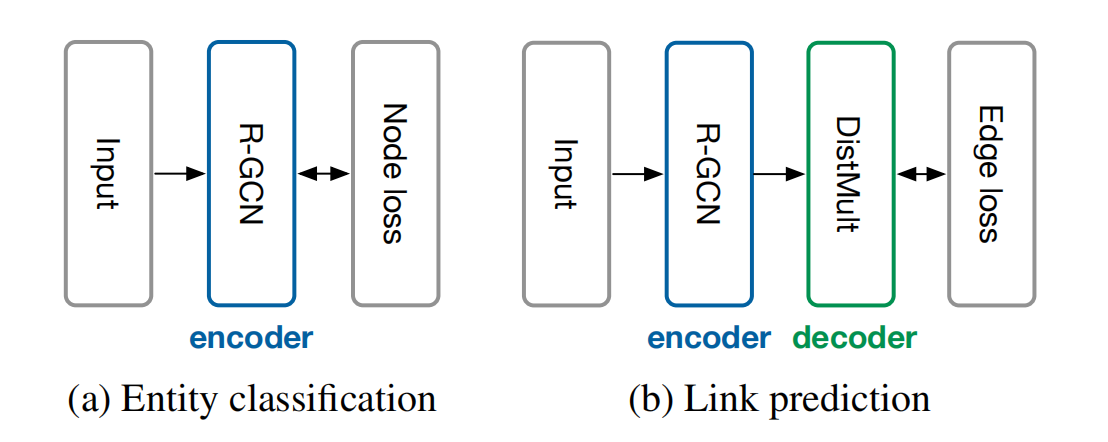
R-GCN的网络结构：

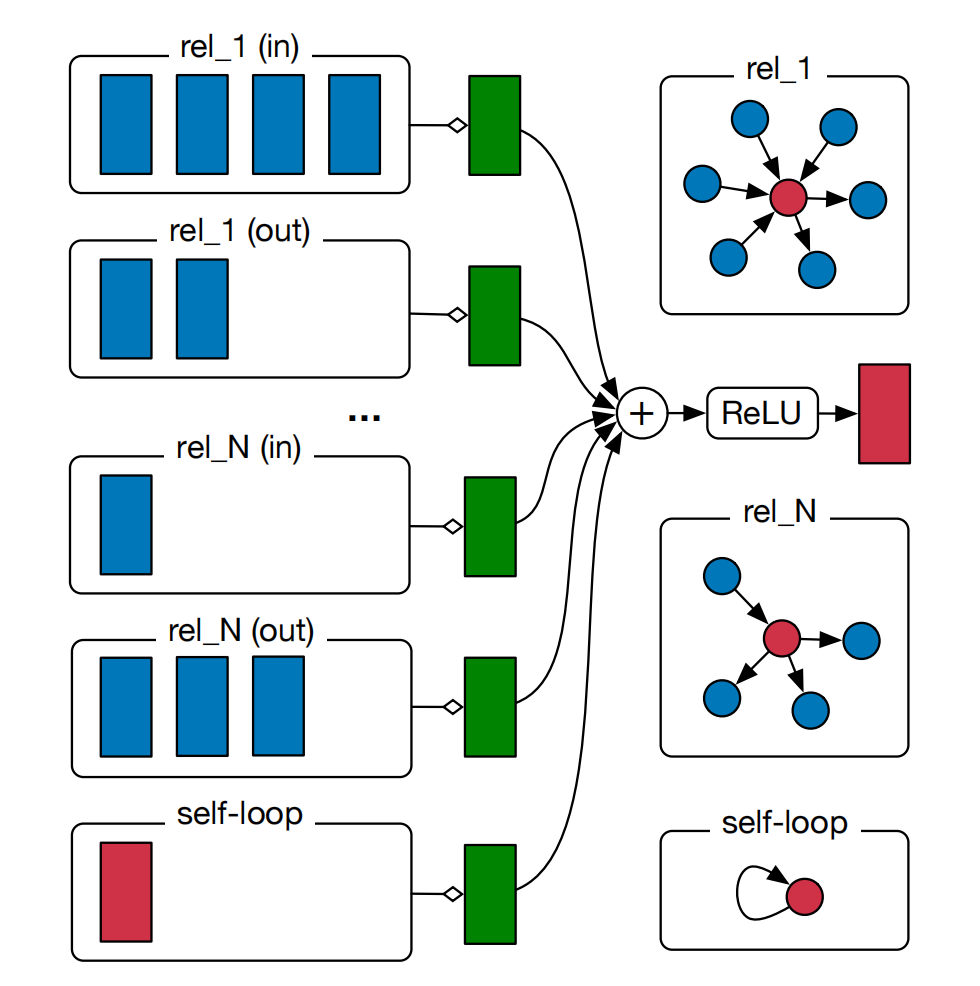
R-GCN引入了由边的类型与方向决定的关系转换，+的后一项表示节点的自连接。红色部分为实体，与蓝色的邻居节点进行矩阵运算，再对每种关系的边类型进行转换，得到绿色部分的已做归一化处理的结果和，累加后经过激活函数传出，并更新模型的节点参数。

针对实体分类来说，只使用了堆叠的 R-GCN 并在最后一层叠加了一个 Softmax 层用于分类；针对关系预测（链接预测）作者考虑使用 DistMult 分解作为评分函数，并使用负采样的训练方式：对于观测样本，考虑ω个负样本，并利用交叉熵损失进行优化。

4.3 推理模型的评判指标

4.3.1 Mean Rank

对于测试集中的每个三元组 (h, r, t)，算法会将其与所有实体和关系的组合进行比较，得到一个排序列表，列表中的第一个三元组应该是正确的三元组。假设正确的三元组排名为rank，那么Mean Rank指标的计算方式为：

Mean Rank = (1/n) * Σrank

其中，n表示测试集中的三元组数量。

4.3.2 Hits@k

Hits@k指标表示算法在前k个最有可能的三元组中是否包含了正确的三元组。具体地，对于测试集中的每个三元组 (h, r, t)，算法会得到一个排名列表，列表中前k个三元组被认为是最有可能的正确答案。如果正确的三元组在前k个三元组中，那么Hits@k的值为1，否则为0。假设测试集中的三元组数量为n，那么Hits@k的计算方式为：

Hits@k = (1/n) * Σ(Indicator(rank <= k))

其中，Indicator是指示函数，当rank <= k时为1，否则为0。

4.3.3 MRR

MRR指标表示算法对于正确三元组的排序效果，具体地，对于测试集中的每个三元组 (h, r, t)，算法会得到一个排序列表，列表中第一个三元组被认为是最有可能的正确答案，其排名为rank。MRR的计算方式为：

MRR = (1/n) * Σ(1/rank)